เมทริกซ์ คือกลุ่มของจำนวนหรือสมาชิกของริงใดๆ เขียนเรียงกันเป็นรูปสี่เหลี่ยมผืนผ้าหรือจัตุรัส กล่าวคือเรียงเป็นแถวในแนวนอน และเรียงเป็นแถวในแนวตั้ง เรามักเขียนเมทริกซ์เป็นตารางที่ไม่มีเส้นแบ่งและเขียนวงเล็บคร่อมตารางไว้ (ไม่ว่าจะเป็นวงเล็บโค้งหรือวงเล็บเหลี่ยม) เช่น
เราเรียกแถวในแนวนอนของเมทริกซ์ว่า แถว เรียกแถวในแนวตั้งของเมทริกซ์ว่า หลัก และเรียกจำนวนแต่ละจำนวนเในเมทริกซ์ว่า สมาชิก ของเมทริกซ์ การกล่าวถึงสมาชิกของเมทริกซ์ จะต้องระบุตำแหน่งให้ถูกต้อง เช่น จากตัวอย่างข้างบน
- สมาชิกที่อยู่ในแถวที่ 2 หลักที่ 3 คือเลข 4
- สมาชิกที่อยู่ในแถวที่ 2 หลักที่ 2 คือเลข 15
- สมาชิกที่อยู่ในแถวที่ 3 หลักที่ 1 คือเลข 5
เราเรียกเมทริกซ์ที่มี 
แถว และ 
หลัก เรียกว่า เมทริกซ์ 
เราเรียกจำนวน และ ว่า มิติ หรือ ขนาด ของเมทริกซ์
แถว และ หลัก เรียกว่า เมทริกซ์ เราเรียกจำนวน และ ว่า มิติ หรือ ขนาด ของเมทริกซ์
เราใช้สัญญลักษณ์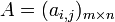 
เพื่อหมายถึง เมทริกซ์ 
ซึ่งมี แถว และ หลัก โดยที่ 
(หรือ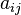 
) หมายถึง สมาชิกที่อยู่ในตำแหน่ง แถว 
และ หลัก 
ของเมทริกซ์ อ่านเพิ่มเติม
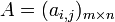เพื่อหมายถึง เมทริกซ์ ซึ่งมี แถว และ หลัก โดยที่ (หรือ 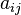) หมายถึง สมาชิกที่อยู่ในตำแหน่ง แถว และ หลัก ของเมทริกซ์ อ่านเพิ่มเติม
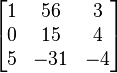
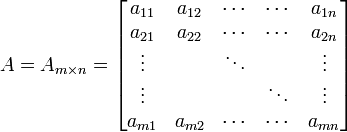
ไม่มีความคิดเห็น:
แสดงความคิดเห็น